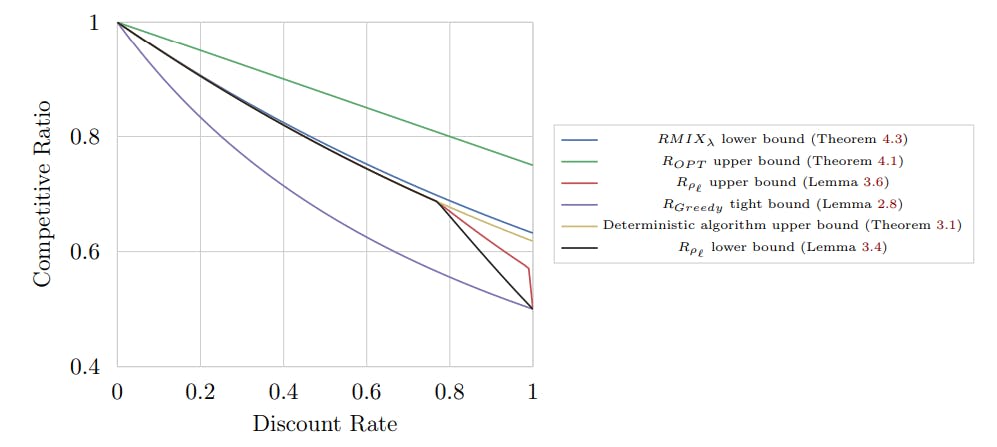
Table of Links
Abstract and 1. Introduction
1.1 Our Approach
1.2 Our Results & Roadmap
1.3 Related Work
-
Model and Warmup and 2.1 Blockchain Model
2.2 The Miner
2.3 Game Model
2.4 Warm Up: The Greedy Allocation Function
-
The Deterministic Case and 3.1 Deterministic Upper Bound
3.2 The Immediacy-Biased Class Of Allocation Function
-
The Randomized Case
-
Discussion and References
- A. Missing Proofs for Sections 2, 3
- B. Missing Proofs for Section 4
- C. Glossary
3 The Deterministic Case
In this section, we focus on the discount model with miner ratio α ̸= 0 and some discount rate λ. Missing proofs are given in Appendix A.
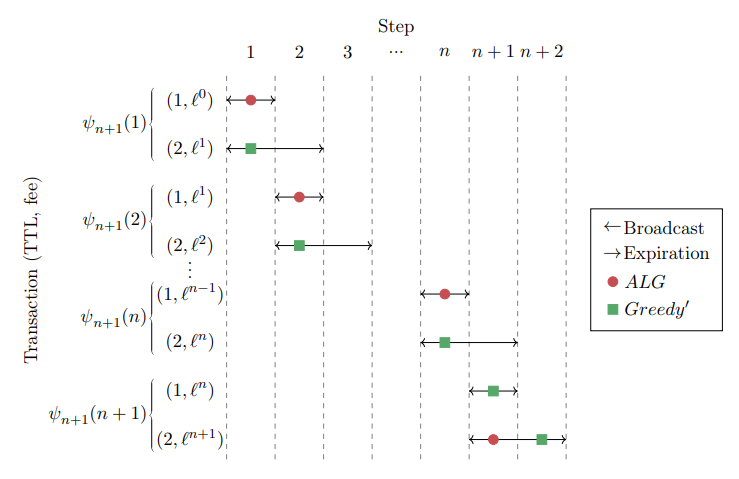
3.1 Deterministic Upper Bound
\
\
\
\
\
\
By combining Eqs. (5) and (6), the proof is concluded:
\
\
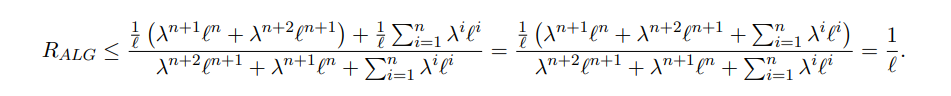
3.2 The Immediacy-Biased Class Of Allocation Function
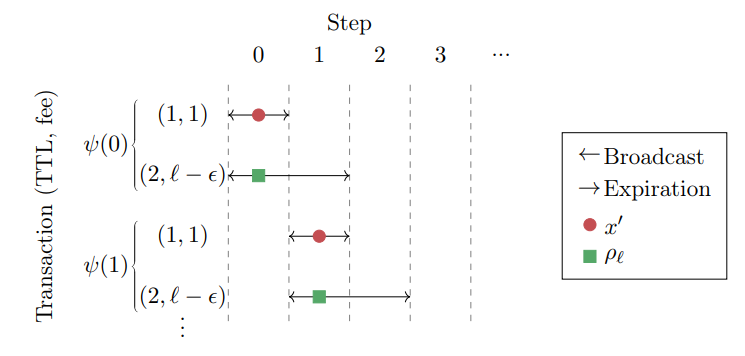
We proceed by introducing the immediacy-biased ratio class of allocation functions, and identify a regime of discount rates λ which we call the “semi-myopic” regime where it achieves the optimal deterministic competitive ratio. Given a parameter ℓ ∈ R, we denote the corresponding instance of this class as ρℓ and define it in the following manner
\
Definition 3.3 (The ℓ-immediacy-biased ratio allocation function ρℓ). For a set S, let
\
\
\
\
Before providing the lower and upper bound analysis, we comment on how our algorithm stands in comparison with another algorithm, MG [LSS05]. While the ℓ-immediacy-biased considers only the highest T T L = 1 transaction as a possible candidate to be scheduled instead of the highest-fee transaction, MG considers any earliest-deadline transaction. I.e., the algorithms differ in their behavior when no T T L = 1 transactions are available. However, in terms of competitive analysis, ℓ-immediacy-biased dominates ℓ-MG. That is because at any case that the ℓ-immediacy-biased allocation chooses a T T L = 1 transaction, ℓ-MG would do the same. But any case that ℓ-immediacy-biased allocation chooses the highest-fee transaction; we can force ℓ-MG to do the same by adding a (1, ϵ) with small enough ϵ to the adversary’s schedule at that step. Therefore, we can force ℓ-MG to make the same choices as ℓ-immediacy-biased allocation, without changing the optimal allocation performance.
\
We bound the allocation function’s competitive ratio from below in Lemma 3.4.
\
\
\
\
\
\
\
4 The Randomized Case
Next, Theorem 4.1 obtains an upper bound on the competitive ratio of any allocation function.
4.1 Randomized Upper Bound
Theorem 4.1. Given α ̸= 0, for any (possibly randomized) allocation function ALG:
\
\
\
\
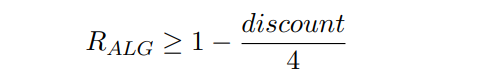
Similarly to the deterministic upper bound, the proof uses a recursive construction of adversaries where the transaction fees grow exponentially. The main technical choice is how to decide the base of the exponent. We guess it by the following equation:
\
\
\
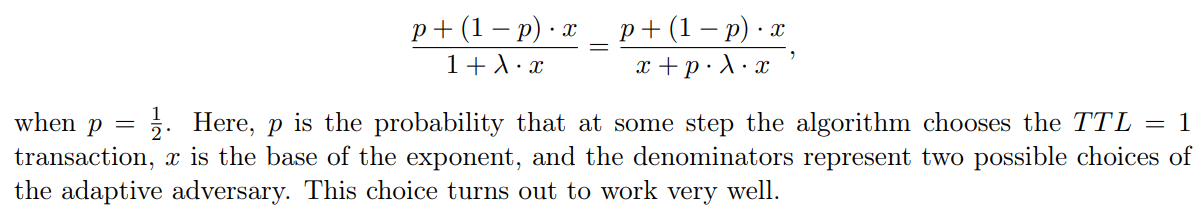
4.2 The RMIXλ Randomized Allocation Function
Next, we show that the best-known randomized allocation function known for the undiscounted case [CCFJST06], extends to the more general discount model.
\
\
\
\
\
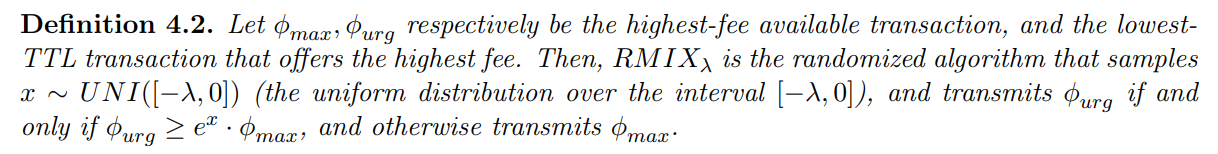
![Figure 5: Bounds for the competitive ratios of Section 3 and Section 4’s various allocation functions, for miners with a mining ratio α ̸= 0 and discount rates λ ∈ [0, 1].](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-xqb324x.png)
\
\
\
\
\
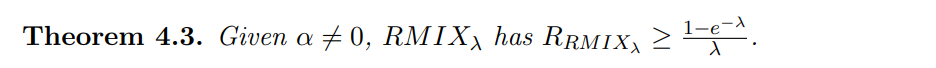
Notably, in the semi-myopic range that we identify in Section 3.2, our simple deterministic allocation achieves very similar performance to the above randomized allocation function.
\
Our competitive ratio results are summarized in Fig. 5.
\
:::info
Authors:
(1) Yotam Gafni, Weizmann Institute (yotam.gafni@gmail.com);
(2) Aviv Yaish, The Hebrew University, Jerusalem (aviv.yaish@mail.huji.ac.il).
:::
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
